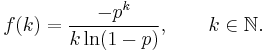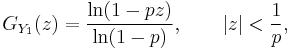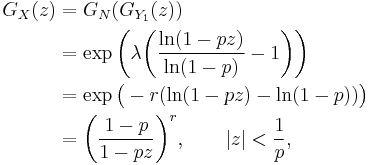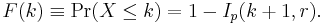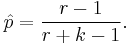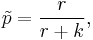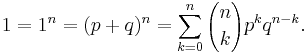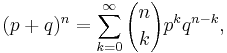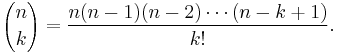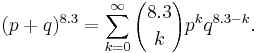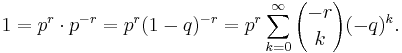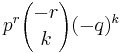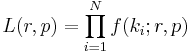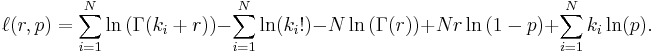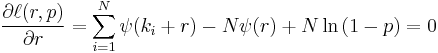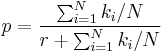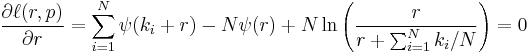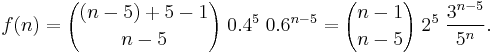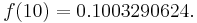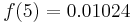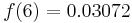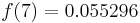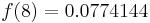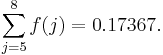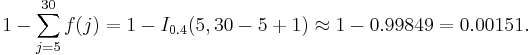Negative binomial distribution
| Probability mass function The orange line represents the mean, which is equal to 10 in each of these plots; the green line shows the standard deviation. |
|
| Notation | 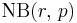 |
|---|---|
| Parameters | r > 0 — number of failures until the experiment is stopped (integer, but the definition can also be extended to reals) p ∈ (0,1) — success probability in each experiment (real) |
| Support | k ∈ { 0, 1, 2, 3, … } |
| PMF | 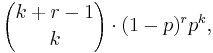 involving a binomial coefficient involving a binomial coefficient |
| CDF | 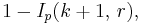 the regularized incomplete beta function the regularized incomplete beta function |
| Mean | 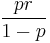 |
| Mode | 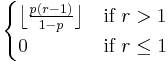 |
| Variance | 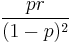 |
| Skewness | 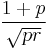 |
| Ex. kurtosis | 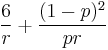 |
| MGF | 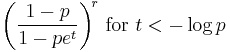 |
| CF | 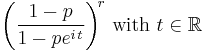 |
| PGF | 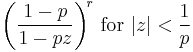 |
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified (non-random) number of failures (denoted r) occur. For example, if one throws a die repeatedly until the third time “1” appears, then the probability distribution of the number of non-“1”s that had appeared will be negative binomial.
The Pascal distribution (after Blaise Pascal) and Polya distribution (for George Pólya) are special cases of the negative binomial. There is a convention among engineers, climatologists, and others to reserve “negative binomial” in a strict sense or “Pascal” for the case of an integer-valued stopping-time parameter r, and use “Polya” for the real-valued case. The Polya distribution more accurately models occurrences of “contagious” discrete events, like tornado outbreaks, than the Poisson distribution.
Contents |
Definition
Suppose there is a sequence of independent Bernoulli trials, each trial having two potential outcomes called “success” and “failure”. In each trial the probability of success is p and of failure is (1 − p). We are observing this sequence until a predefined number r of failures has occurred. Then the random number of successes we have seen, X, will have the negative binomial (or Pascal) distribution:
When applied to real-world situations, the words success and failure need not necessarily be associated with outcomes which we see as good or bad. Say in one case we may use the negative binomial distribution to model the number of days a certain machine works before it breaks down. In such a case “success” would mean the machine was working properly, whereas “failure” would mean it broke down. In another case we can use the negative binomial distribution to model the number of attempts needed for a sportsman to score a goal. Then “failure” would be his/her scoring the goal, whereas “successes” are misses.
The probability mass function of the negative binomial distribution is
Here the quantity in parentheses is called the binomial coefficient, and is equal to
This quantity can alternatively be written in the following manner, explaining the name “negative binomial”:
To understand the above definition of the probability mass function, note that the probability for every specific sequence of k successes and r failures is (1 − p)rpk, because the outcomes of the k + r trials are supposed to happen independently. Since the rth failure comes last, it remains to choose the k trials with successes out of the remaining k + r − 1 trials. The above binomial coefficient, due to its combinatorial interpretation, gives precisely the number of all these sequences of length k + r − 1.
Extension to real-valued r
It is possible to extend the definition of the negative binomial distribution to the case of a positive real parameter r. Although it is impossible to visualize a non-integer number of “failures”, we can still formally define the distribution through its probability mass function.
As before, we say that X has a negative binomial (or Pólya) distribution if it has a probability mass function:
Here r is a real, positive number. The binomial coefficient is then defined by the multiplicative formula and can also be rewritten using the gamma function:
Note that by the binomial series and (*) above, for every 0 ≤ p < 1,
hence the terms of the probability mass function indeed add up to one.
Alternative formulations
Some textbooks may define the negative binomial distribution slightly differently than it is done here. The most common variations are:
- The definition where X is the total number of trials needed to get r failures, not simply the number of successes. Since the total number of trials is equal to the number of successes plus the number of failures, this definition differs from ours by adding constant r. In order to convert formulas written with this definition into the one used in the article, replace everywhere “k” with “k - r”, and also subtract r from the mean, the median, and the mode. In order to convert formulas of this article into this alternative definition, replace “k” with “k + r” and add r to the mean, the median and the mode. Effectively, this implies using the probability mass function
- The definition where p denotes the probability of a failure, not of a success. This may also be formulated as “X is the number of failures before r successes”, in which case p will be the probability of a success, but the words “failure” and “success” have been swapped around. In order to convert formulas between this definition and the one used in the article, replace “p” with “1 − p” everywhere.
- The two alterations above may be applied simultaneously.
Occurrence
Waiting time in a Bernoulli process
For the special case where r is an integer, the negative binomial distribution is known as the Pascal distribution. It is the probability distribution of a certain number of failures and successes in a series of independent and identically distributed Bernoulli trials. For k + r Bernoulli trials with success probability p, the negative binomial gives the probability of k successes and r failures, with a failure on the last trial. In other words, the negative binomial distribution is the probability distribution of the number of successes before the rth failure in a Bernoulli process, with probability p of successes on each trial. A Bernoulli process is a discrete time process, and so the number of trials, failures, and successes are integers.
Consider the following example. Suppose we repeatedly throw a die, and consider a “1” to be a “failure”. The probability of failure on each trial is 1/6. The number of successes before the third failure belongs to the infinite set { 0, 1, 2, 3, ... }. That number of successes is a negative-binomially distributed random variable.
When r = 1 we get the probability distribution of number of successes before the first failure (i.e. the probability of the first failure occurring on the (k + 1)st trial), which is a geometric distribution:
Overdispersed Poisson
The negative binomial distribution, especially in its alternative parameterization described above, can be used as an alternative to the Poisson distribution. It is especially useful for discrete data over an unbounded positive range whose sample variance exceeds the sample mean. In such cases, the observations are overdispersed with respect to a Poisson distribution, for which the mean is equal to the variance. Hence a Poisson distribution is not an appropriate model. Since the negative binomial distribution has one more parameter than the Poisson, the second parameter can be used to adjust the variance independently of the mean. See Cumulants of some discrete probability distributions. An application of this is to annual counts of tropical cyclones in the North Atlantic or to monthly to 6-monthly counts of wintertime extratropical cyclones over Europe, for which the variance is greater than the mean.[1][2][3] In the case of modest overdispersion, this may produce substantially similar results to an overdispersed Poisson distribution.[4][5]
Related distributions
- The geometric distribution (on { 0, 1, 2, 3, ... }) is a special case of the negative binomial distribution, with
- The negative binomial distribution is a special case of the discrete phase-type distribution.
Poisson distribution
Consider a sequence of negative binomial distributions where the stopping parameter r goes to infinity, whereas the probability of success in each trial, p, goes to zero in such a way as to keep the mean of the distribution constant. Denoting this mean λ, the parameter p will have to be
Under this parametrization the probability mass function will be
Now if we consider the limit as r → ∞, the second factor will converge to one, and the third to the exponent function:
which is the mass function of a Poisson-distributed random variable with expected value λ.
In other words, the alternatively parameterized negative binomial distribution converges to the Poisson distribution and r controls the deviation from the Poisson. This makes the negative binomial distribution suitable as a robust alternative to the Poisson, which approaches the Poisson for large r, but which has larger variance than the Poisson for small r.
Gamma–Poisson mixture
The negative binomial distribution also arises as a continuous mixture of Poisson distributions where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed according to Gamma(r, p/(1 − p)).
Formally, this means that the mass function of the negative binomial distribution can be written as
Because of this, the negative binomial distribution is also known as the gamma–Poisson (mixture) distribution.
Sum of geometric distributions
If Yr is a random variable following the negative binomial distribution with parameters r and p, and support {0, 1, 2, ...}, then Yr is a sum of r independent variables following the geometric distribution (on { 0, 1, 2, 3, ... }) with parameter 1 − p. As a result of the central limit theorem, Yr (properly scaled and shifted) is therefore approximately normal for sufficiently large r.
Furthermore, if Bs+r is a random variable following the binomial distribution with parameters s + r and 1 − p, then
In this sense, the negative binomial distribution is the "inverse" of the binomial distribution.
The sum of independent negative-binomially distributed random variables r1 and r2 with the same value for parameter p is negative-binomially distributed with the same p but with "r-value" r1 + r2.
The negative binomial distribution is infinitely divisible, i.e., if Y has a negative binomial distribution, then for any positive integer n, there exist independent identically distributed random variables Y1, ..., Yn whose sum has the same distribution that Y has.
Representation as compound Poisson distribution
The negative binomial distribution NB(r,p) can be represented as a compound Poisson distribution: Let {Yn, n ∈ ℕ0} denote a sequence of independent and identically distributed random variables, each one having the logarithmic distribution Log(p), with probability mass function
Let N be a random variable, independent of the sequence, and suppose that N has a Poisson distribution with parameter λ = −r ln(1 − p). Then the random sum
is NB(r,p)-distributed. To prove this, we calculate the probability generating function GX of X, which is the composition of the probability generating functions GN and GY1. Using
and
we obtain
which is the probability generating function of the NB(r,p) distribution.
Properties
Cumulative distribution function
The cumulative distribution function can be expressed in terms of the regularized incomplete beta function:
Sampling and point estimation of p
Suppose p is unknown and an experiment is conducted where it is decided ahead of time that sampling will continue until r successes are found. A sufficient statistic for the experiment is k, the number of failures.
In estimating p, the minimum variance unbiased estimator is
The maximum likelihood estimate of p is
but this is a biased estimate. Its inverse (r + k)/r, is an unbiased estimate of 1/p, however.[6]
Relation to the binomial theorem
Suppose Y is a random variable with a binomial distribution with parameters n and p. Assume p + q = 1, with p, q >=0. Then the binomial theorem implies that
Using Newton's binomial theorem, this can equally be written as:
in which the upper bound of summation is infinite. In this case, the binomial coefficient
is defined when n is a real number, instead of just a positive integer. But in our case of the binomial distribution it is zero when k > n. We can then say, for example
Now suppose r > 0 and we use a negative exponent:
Then all of the terms are positive, and the term
is just the probability that the number of failures before the rth success is equal to k, provided r is an integer. (If r is a negative non-integer, so that the exponent is a positive non-integer, then some of the terms in the sum above are negative, so we do not have a probability distribution on the set of all nonnegative integers.)
Now we also allow non-integer values of r. Then we have a proper negative binomial distribution, which is a generalization of the Pascal distribution, which coincides with the Pascal distribution when r happens to be a positive integer.
Recall from above that
- The sum of independent negative-binomially distributed random variables r1 and r2 with the same value for parameter p is negative-binomially distributed with the same p but with "r-value" r1 + r2.
This property persists when the definition is thus generalized, and affords a quick way to see that the negative binomial distribution is infinitely divisible.
Parameter estimation
Maximum likelihood estimation
The likelihood function for N iid observations (k1, ..., kN) is
from which we calculate the log-likelihood function
To find the maximum we take the partial derivatives with respect to r and p and set them equal to zero:
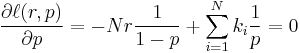 and
and
where
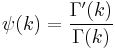 is the digamma function.
is the digamma function.
Solving the first equation for p gives:
Substituting this in the second equation gives:
This equation cannot be solved in closed form. If a numerical solution is desired, an iterative technique such as Newton's method can be used.
Examples
Selling candy
Pat is required to sell candy bars to raise money for the 6th grade field trip. There are thirty houses in the neighborhood, and Pat is not supposed to return home until five candy bars have been sold. So the child goes door to door, selling candy bars. At each house, there is a 0.4 probability of selling one candy bar and a 0.6 probability of selling nothing.
What's the probability of selling the last candy bar at the nth house?
Recall that the NegBin(r, p) distribution describes the probability of k failures and r successes in k + r Bernoulli(p) trials with success on the last trial. Selling five candy bars means getting five successes. The number of trials (i.e. houses) this takes is therefore k + 5 = n. The random variable we are interested in is the number of houses, so we substitute k = n − 5 into a NegBin(5, 0.4) mass function and obtain the following mass function of the distribution of houses (for n ≥ 5):
What's the probability that Pat finishes on the tenth house?
What's the probability that Pat finishes on or before reaching the eighth house?
To finish on or before the eighth house, Pat must finish at the fifth, sixth, seventh, or eighth house. Sum those probabilities:
What's the probability that Pat exhausts all 30 houses in the neighborhood?
This can be expressed as the probability that Pat does not finish on the fifth through the thirtieth house:
Polygyny in African societies
Data on polygyny among a wide range of traditional African societies suggest that the distribution of wives follow a range of binomial profiles. The majority of these are negative binomial indicating the degree of competition for wives. However some tend towards a Poisson Distribution and even beyond towards a true binomial, indicating a degree of conformity in the allocation of wives. Further analysis of these profiles indicates shifts along this continuum between more competitiveness or more conformity according to the age of the husband and also according to the status of particular sectors within a society. In this way, these binomial distributions provide a tool for comparison, between societies, between sectors of societies, and over time.[7]
See also
- Coupon collector's problem
- Beta negative binomial distribution
- Extended negative binomial distribution
- Negative multinomial distribution
- Binomial distribution
- Poisson distribution
References
- ^ Villarini, G.; Vecchi, G.A. and Smith, J.A. (2010). "Modeling of the dependence of tropical storm counts in the North Atlantic Basin on climate indices". Monthly Weather Review 138 (7): 2681–2705. doi:10.1175/2010MWR3315.1.
- ^ Mailier, P.J.; Stephenson, D.B.; Ferro, C.A.T.; Hodges, K.I. (2006). "Serial Clustering of Extratropical Cyclones". Monthly Weather Review 134 (8): 2224–2240. doi:10.1175/MWR3160.1.
- ^ Vitolo, R.; Stephenson, D.B.; Cook, Ian M.; Mitchell-Wallace, K. (2009). "Serial clustering of intense European storms". Meteorologische Zeitschrift 18 (4): 411–424. doi:10.1127/0941-2948/2009/0393.
- ^ McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Boca Raton: Chapman and Hall/CRC. ISBN 0-412-31760-5.
- ^ Cameron, Adrian C.; Trivedi, Pravin K. (1998). Regression analysis of count data. Cambridge University Press. ISBN 0-521-63567-5.
- ^ J. B. S. Haldane, "On a Method of Estimating Frequencies", Biometrika, Vol. 33, No. 3 (Nov., 1945), pp. 222–225. JSTOR 2332299
- ^ Spencer, Paul, 1998, The Pastoral Continuum: the Marginalization of Tradition in East Africa, Clarendon Press, Oxford (pp. 51-92).
Further reading
- Hilbe, Joseph M., Negative Binomial Regression, Cambridge, UK: Cambridge University Press (2007) Negative Binomial Regression – Cambridge University Press
|
|||||||||||
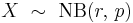
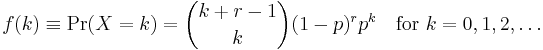
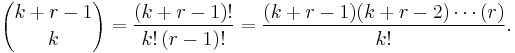
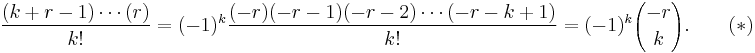
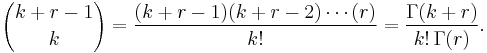
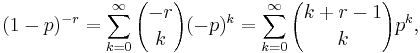
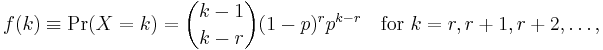
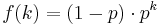
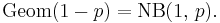
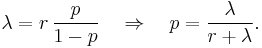
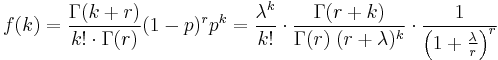
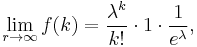
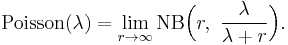
![\begin{align}
f(k) & = \int_0^\infty f_{\text{Poisson}(\lambda)}(k) \cdot f_{\text{Gamma}\left(r,\, \frac{p}{1-p}\right)}(\lambda) \; \mathrm{d}\lambda \\[8pt]
& = \int_0^\infty \frac{\lambda^k}{k!} e^{-\lambda} \cdot \lambda^{r-1}\frac{e^{-\lambda (1-p)/p}}{\big(\frac{p}{1-p}\big)^r\,\Gamma(r)} \; \mathrm{d}\lambda \\[8pt]
& = \frac{(1-p)^r p^{-r}}{k!\,\Gamma(r)} \int_0^\infty \lambda^{r%2Bk-1} e^{-\lambda/p} \;\mathrm{d}\lambda \\[8pt]
& = \frac{(1-p)^r p^{-r}}{k!\,\Gamma(r)} \ p^{r%2Bk} \, \Gamma(r%2Bk) \\[8pt]
& = \frac{\Gamma(r%2Bk)}{k!\;\Gamma(r)} \; (1-p)^r p^k.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/62bd950c0ae31e1d29278caf9583d195.png)